¡Fuerzas Conservativas!

Energía Potencial:

La energía potencial es el otro tipo de energía mecánica que pueden tener los cuerpos. A diferencia de la energía cinética, la energía potencial está asociada a la posición que tienen los cuerpos, y no a su movimiento.

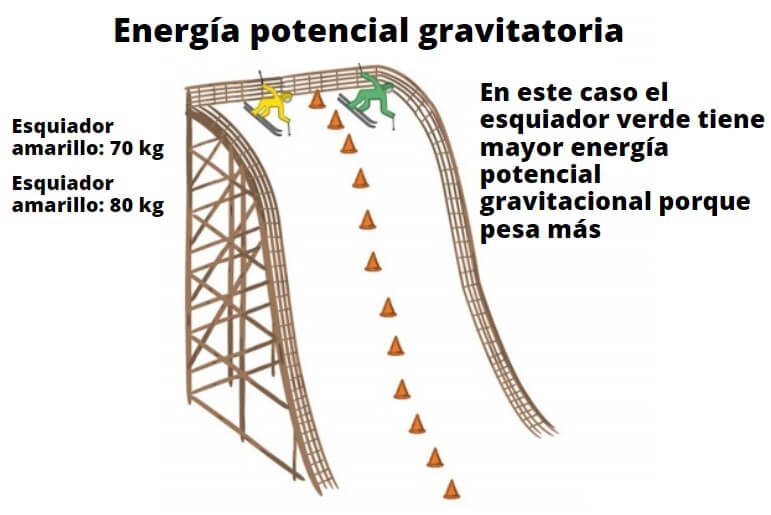
Energía Potencial Gravitatoria:

¿Cómo se obtiene la fórmula de la Energía Potencial Gravitatoria?

Para obtener el valor de la energía potencial gravitatoria razonamos de la siguiente manera.

Vamos a elevar un cuerpo desde el suelo h1 = 0 a una altura h2 = h

Para elevar el cuerpo, debemos ejercer una fuerza igual (al menos) a su peso. Con esto conseguimos que el cuerpo ascienda con velocidad constante hasta la altura h, no variando en ningún momento su energía cinética

El valor del trabajo realizado por nosotros sobre el cuerpo:

W1→2=F→⋅Δr→=F⋅Δh⋅cos(0)=m⋅g⋅Δh=m⋅g⋅h2−m⋅g⋅h1=m⋅g⋅h

Donde hemos tenido en cuenta que P = m·g es el peso

 

El cuerpo que ha recibido el trabajo, ha adquirido energía, considerando que el trabajo que realiza una fuerza sobre un cuerpo es igual a su variación de energía y que el cuerpo al encontrarse en el suelo no tenía energía E1 = 0, nos queda:

W=E2−E1⇒W=E2=m⋅g⋅h

Trabajo Realizado por la Fuerza Gravitacional o Peso:

Si queremos calcular el trabajo realizado por la fuerza gravitacional (peso) sobre un cuerpo que se encuentra a cierta altura h y se deja caer hasta el suelo, debemos de tener en cuenta que:

Será la Tierra la que realizará el trabajo sobre el cuerpo a través del peso

P→=−m⋅g⋅j→

El desplazamiento también es vertical y su valor viene dado por:

Δr→=−j→⋅(h−h suelo)

Con todo lo anterior nos queda:

W=F→⋅Δr→=(−j)⋅m⋅g⋅(h−h suelo)⋅(−j)=m⋅g⋅(h−h suelo)

Δh=h final−h inicial=h suelo−h

Finalmente, con estas dos expresiones podemos concluir que:

W=m⋅g⋅(h−h suelo)=−m⋅g⋅Δh=−ΔEp

Es decir, el trabajo realizado por la fuerza (peso), es igual a la variación negativa de la energía potencial del cuerpo.

 

La energía potencial gravitatoria cumple con las siguientes características:

1. Para que exista energía potencial gravitatoria tiene que existir la gravedad. Sin gravedad, todas las posiciones de un cuerpo serían equivalentes.
2. El valor de la energía potencial en un punto es relativo. Depende del nivel de referencia elegido para la altura.
3. Puede ser positiva o negativa, según donde se sitúe el nivel 0 de altura.
4. La diferencia de energía potencial ∆Ep entre dos puntos es un valor absoluto, que coincide con el trabajo necesario para llevar el cuerpo desde el primer punto hasta el segundo y es independiente del sistema de referencia elegido.
5. Se incrementa con la altura.
6. La expresión Ep = m·g·h sólo es válida para alturas pequeñas, donde podemos considerar g constante ya que, en realidad, g varía con la altura.
7.  Definimos la energía potencial elástica como aquella que adquieren los cuerpo sometidos a la acción de fuerzas elásticas o recuperadoras.

Ejemplo:

 

Energía potencial elástica:

La energía potencial elástica se refiere a la energía almacenada que resulta de aplicar una fuerza para deformar un objeto elástico. La energía queda almacenada hasta que se quita la fuerza y el objeto elástico regresa a su forma original, haciendo un trabajo en el proceso. La deformación puede implicar comprimir, estirar o retorcer el objeto.

Muchos objetos están diseñados específicamente para almacenar energía potencial elástica, por ejemplo:

• El muelle de un reloj de cuerda.
• Un arquero que estira su arco.
• Un trampolín doblado justo antes de que el clavadista brinque.
• La liga de hule de una resortera.

Un objeto diseñado para almacenar energía potencial elástica usualmente tendrá un límite elástico alto, sin embargo, todos los objetos elásticos tienen un límite para la carga que pueden soportar. Cuando la deformación va más allá del límite elástico, el objeto ya no vuelve a su forma original.

¿Cómo se obtiene la fórmula de la Energía Potencial Elástica?

Vamos a comprimir o estirar un muelle desde su posición de equilibrio (x1 = 0) a posición una posición x2 = x. Consideraremos que el muelle no tiene energía inicial (E1 = 0) por encontrarse en su posición de equilibrio

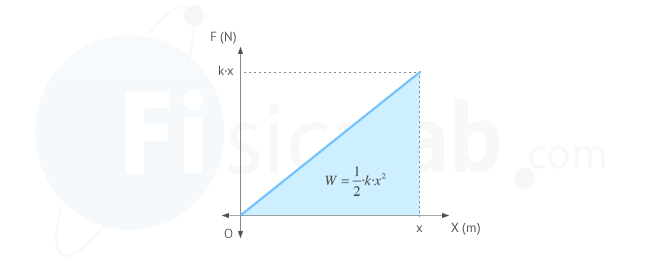
Para comprimir o estirar el muelle hemos de ejercer una fuerza igual en magnitud, pero de sentido contrario a la ley de Hooke. F→=k⋅x→

La fuerza ejercida es variable, siendo prácticamente nula al principio y aumentando a medida que aumenta x

Para calcular el trabajo ejercido por nosotros sobre el muelle, calculamos el área del triángulo limitado por la curva.

W0→x=12⋅k⋅x⋅x=12⋅k⋅x2

El muelle, sobre el que hemos realizado el trabajo, ha adquirido energía. Considerando que el trabajo que realiza una fuerza sobre un cuerpo es igual a su variación de energía y que el cuerpo al encontrarse en la posición de equilibrio x = 0 no tenía energía, nos queda que de modo que

 

W=E2−E1⇒E2=12⋅k⋅x2

Ejemplo:

 

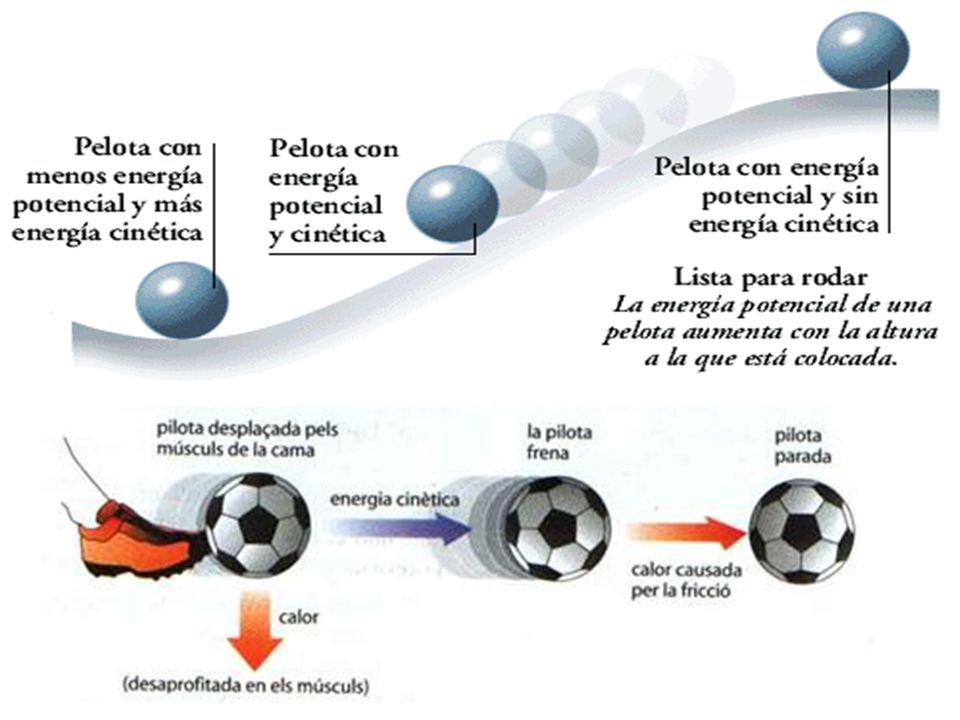
 Conservación de la Energía: 

El Principio de conservación de la energía indica que la energía no se crea ni se destruye; sólo se transforma de unas formas a otras. En estas transformaciones, la energía total permanece constante; es decir, la energía total es la misma antes y después de cada transformación.

En el caso de la energía mecánica se puede concluir que, en ausencia de rozamientos y sin intervención de ningún trabajo externo, la suma de las energías cinética y potencial permanece constante. Este fenómeno se conoce con el nombre de Principio de conservación de la energía mecánica; es decir, la energía cinética más la energía potencial en cualquier instante de la trayectoria es la misma; por ejemplo, la fuerza gravitacional, pues en cualquier trabajo que realice un cuerpo contra la fuerza de gravedad de la Tierra, la energía se recuperará íntegramente cuando el cuerpo descienda.

Em = Ec + Ep

Donde Em = energía mecánica total expresada en Joules. Sustituyendo las expresiones de las energías:

Em = 1/2mv2 + mgh

En resumen, "la energía existente en un sistema es una cantidad constante que no se crea ni se destruye, únicamente se transforma". Respecto de fuerzas no conservativas (por ejemplo, la fricción) no podemos hablar de energía potencial; sin embargo, la conservación de la energía se mantiene en la forma:

Em = Ec + Q donde Q es ahora el calor disipado al ambiente, en este caso la EC disminuye siempre y eventualmente el calor transporta la energía a la atmósfera.